【翻译活动】面向数据科学的概率论-14.中心极限定律

十四、 中心极限定律

原文：prob140/textbook/notebooks/ch_14

译者：喵十八

协议：CC BY-NC-SA 4.0

自豪地采用谷歌翻译

本章依赖的python

# HIDDEN
from datascience import *
from prob140 import *
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
%matplotlib inline
from scipy import stats

# HIDDEN
def dist_sum(n, probs_0_through_N):
    """Return the distribution of S_n,
    the sum of n i.i.d. copies
    of a random variable with distribution probs_0_through_N
    on the integers 0, 1, 2, ..., N"""
    
    # Find the possible values of S_n
    N = len(probs_0_through_N) - 1   
    values_Sn = np.arange(n*N + 1)
    
    # Find the probailities of those values
    coeffs_X1 = np.flipud(probs_0_through_N)
    pgf_X1 = np.poly1d(coeffs_X1)
    pgf_Sn = pgf_X1**n
    coeffs_Sn = pgf_Sn.c
    probs_Sn = np.flipud(coeffs_Sn)
    
    t = Table().with_columns(
        'Value', values_Sn,
        'Probability', probs_Sn
    )
    return t

中心极限定理

标准差是广为流传的衡量标准之一，此外，还有很多其他的衡量标准。为什么使用标准差？主要的原因是标准差和正态曲线之间的联系。为何正态曲线如此重要？本章将回答该问题。

我们将从分析一个独立同分布的概率和开始。并已知其均值和标准差。在本章中，我们将研究分布的形状：当我们可以计算它的精确形状时，我们计算它，当数据量过大时，我们计算一个其近似值。

精确分布

我们已经知道如何找到任意两个离散随机变量之和的分布。

$$P(X+Y = k) = \sum_j P(X=j, Y=k-j)$$

如果$X$和$Y$是独立的，这简化为成为离散卷积公式：

$$P(X+Y = k) = \sum_j P(X=j)P(Y=k-j)$$

通过归纳，我们可以将其扩展到任何有限数量的自变量的和。

所以原则上讲，我们知道如何找到$n$个（$n > 1$）独立随机变量的概率分布之和。但是，对于很大的$n$，这种方式很难实现。

在本节中，我们将研究另一种分布求和的方法。正如您将看到的，它更容易实现自动化，但最终也会遇到计算障碍。

概率生成函数

设$X$是一个随机变量，对于给定的$N$，其可能取值为$0, 1, 2, \ldots, N$。
为简洁起见，令$p_k = P(X = k)$，其中$k$的取值范围为0到$N$。

定义$X$的概率生成函数(pgf)为

$$G_X(s) ~ = ~ \sum_{k=0}^N p_ks^k, ~~~ -\infty < s < \infty$$

对于具有无限多个非负整数随机变量的扩展，请参阅本节末尾的技术说明。

上面的定义表明对任何$s$，有

$$G_X(s) ~ = ~ p_0 + p_1s + p_2s^2 + p_3s^3 + \cdots + p_Ns^N$$

你可以看到$G_X$是一个$N$次多项式，并且$s^k$的系数是$p_k = P(X=k)$。

因此，如果给你一个随机变量的pgf，你可以通过简单地列出所有的权重和相应的系数来计算出随机变量的分布。

要了解这如何帮助我们找到总和的分布，请观察每一个$s$，$G_X(s)$的期望为

$$G_X(s) ~ = ~ \sum_{k=0}^N s^kP(X=k) ~ = ~ E(s^X)$$

因此，如果$X$和$Y$是独立的非负整数随机变量，那么对于每个$s$有

$$G_{X+Y}(s) ~ = ~ E(s^{X+Y}) ~ = ~ E(s^X s^Y) ~ = ~ E(s^X)E(s^Y) ~ = ~ G_X(s)G_Y(s)$$

我们已经使用了这样的事实：对于独立的随机变量，其相乘的期望是期望的相乘。

结果表明两个独立随机变量之和的pgf是两个pgf的乘积。这很容易扩展到两个以上的随机变量，并为独立同分布变量之和的pgf产生一个简单的公式。

一个独立同分布样本分布之和的PGF

设$X_1, X_2, \ldots, X_n$是分布在$0, 1, 2, \ldots, N$上的独立同分布事件。令$S_n = X_1 + X_2 + \cdots + X_n$，那么$S_n$的pgf为：

$$G_{S_n}(s) ~ = ~ \big{(}G_{X_1}(s)\big{)}^n, ~~~ -\infty < s < \infty$$

因为$G{X_1}$是一个$N$次多项式，$G{S_n}$也是一个$nN$次多项式。与任何pgf一样，$s^k$的系数是$k$的概率。也就是说，对于每一个在0到$nN$范围内的$k$有

$$P(S_n = k) = \text{coefficient of } s^k \text{ in } G_{S_n}(s)$$

我们现在有一个查找$S_n$分布的算法。

• 从$X_1$的pgf开始。
• 增加幂至$n$。也就是$S_n$的pgf。
• 读取$S_n$的pgf.

精彩！我们完成了！除了实际上这样做涉及将多项式升幂。当数很大时，这是一项艰巨的任务。

幸运的是，正如您将在下一节中看到的那样，NumPy使用一组多项式方法来解决问题。

技术说明。我们已经为具有有限多个非负整数值的随机变量定义了概率生成函数。该定义可以扩展到具有无限多个非负整数值的随机变量。但在这种情况下，pgf是一个无限系列，我们必须小心收敛。通常，pdf是的值域 $|s| \le 1$，这样它就会收敛。

NumPy中的PGF

回忆一下，我们找到$S_n$分布的算法。

• 从$X_1$的pgf开始。
• 增加幂至$n$。也就是$S_n$的pgf。
• 读取$S_n$的pgf.

在本节中，我们将使用NumPy实践此算法。

假设$X_1$的分布为$p_0 = 0.1$，$p_1 = 0.5$，$p_2 = 0.4$。令数组probs_X1包含了0,1,2的概率。

probs_X1 = make_array(0.1, 0.5, 0.4)

dist_X1 = Table().values(np.arange(3)).probability(probs_X1)
Plot(dist_X1)

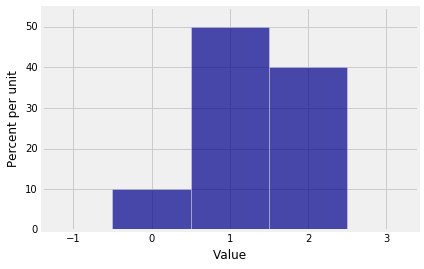
$X_1$的pgf是：

$$0.1 + 0.5s + 0.4s^2$$

NumPy 以标准的数学方式表示这个多项式，以最高次项开始：

$$0.4s^2 + 0.5s + 0.1$$

方法np.flipud将概率数组反转为与该系数的顺序一致。ud代表“up down”。NumPy正在考虑将数组作为一个列。NumPy考虑将该数组转为一列。

coeffs_X1 = np.flipud(probs_X1)
coeffs_X1

array([ 0.4,  0.5,  0.1])

方法np.poly1d以系数数组为参数，构造多项式。方法名中的1d代表”一维”。

pgf_X1 = np.poly1d(coeffs_X1)
print(pgf_X1)

     2
0.4 x + 0.5 x + 0.1

调用print方法，打印出该多项式。在$s$的位置，用$x$代替表示。请记住，最后一项是$x^0$的系数。

现在假设$S_3$是三个$X_1$副本的和。$S_3$的pgf是$X_1$pgf的三次方，并且可以按照您的希望计算。

pgf_S3 = pgf_X1**3
print(pgf_S3)

       6        5         4         3         2
0.064 x + 0.24 x + 0.348 x + 0.245 x + 0.087 x + 0.015 x + 0.001

$S_3$中多项式的幂为从0到6，因为$S_3$是三个幂从0到2的值的副本的和。系数是$S_3$分布的概率。

你可以使用属性c输出其“系数”。

coeffs_S3 = pgf_S3.c
coeffs_S3

array([ 0.064,  0.24 ,  0.348,  0.245,  0.087,  0.015,  0.001])

这些是从6次到0次项的系数。在概率中，更习惯从低到高的顺序来看，所以再使用一次np.flipud：

probs_S3 = np.flipud(coeffs_S3)
probs_S3

array([ 0.001,  0.015,  0.087,  0.245,  0.348,  0.24 ,  0.064])

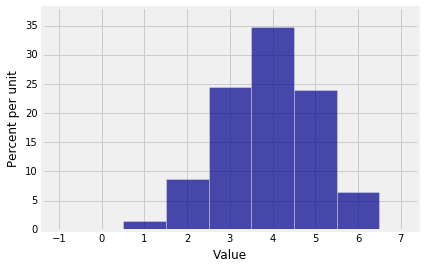
您现在拥有绘制$S_3$的概率直方图所需的输入了

dist_S3 = Table().values(np.arange(7)).probability(probs_S3)
Plot(dist_S3)

计算分布$S_n$的函数

我们将结合上面的步骤来创建一个函数dist_sum，入参为副本个数$n$和$X_1$的分布，返回值为$n$个$X_1$的副本的和的分布。

def dist_sum(n, probs_0_through_N):
    """Return the distribution of S_n,
    the sum of n i.i.d. copies
    of a random variable with distribution probs_0_through_N
    on the integers 0, 1, 2, ..., N"""
    
    # Find the possible values of S_n
    N = len(probs_0_through_N) - 1   
    values_Sn = np.arange(n*N + 1)
    
    # Find the probailities of those values
    coeffs_X1 = np.flipud(probs_0_through_N)
    pgf_X1 = np.poly1d(coeffs_X1)
    pgf_Sn = pgf_X1**n
    coeffs_Sn = pgf_Sn.c
    probs_Sn = np.flipud(coeffs_Sn)
    
    t = Table().with_columns(
        'Value', values_Sn,
        'Probability', probs_Sn
    )
    return t

$n$次掷骰子游戏的和

在第3章中，我们通过列出所有的$6^5$种可能情况，并计算他们从而找到了5次掷骰子游戏的和的分布。这种方法难以处理大数据量的情况。让我们看看我们的新方法是否可以找到10个骰子总和的分布。

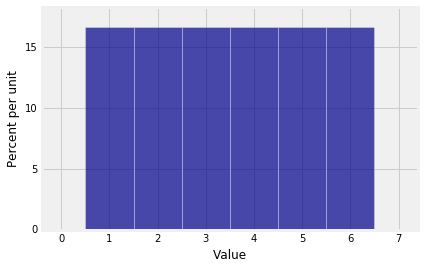
我们必须从单个筛子的分布开始，为此重要的是要记住包含0作为0个点的概率。否则pgf将是错误的，因为NumPy不知道它不应该包括0次项。

die = np.append(0, (1/6)*np.ones(6))
die

array([ 0.        ,  0.16666667,  0.16666667,  0.16666667,  0.16666667,
        0.16666667,  0.16666667])

Plot(dist_sum(1, die))

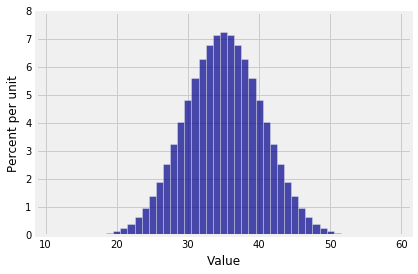
Plot(dist_sum(10, die))

制作波

10个筛子和的分布，看上去很符合正态分布。是所有的和都这样么？

要探索这个问题，让$X_1$的分布为$p_1 = p_2 = p_9 = 1/3$

probs_X1 = make_array(0, 1/3, 1/3, 0, 0, 0, 0, 0, 0, 1/3)

这是$X_1$的分布。

Plot(dist_sum(1, probs_X1))

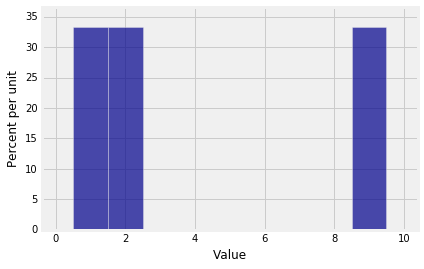
$S_{10}$的概率直方图表明“和”并不总是具有平滑的分布。

Plot(dist_sum(10, probs_X1))

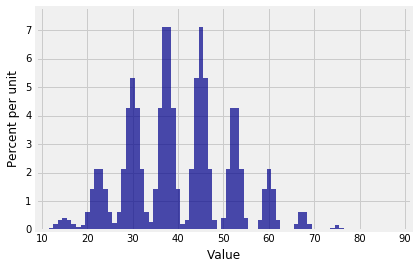
$S_{30}$的分布看上去头发乱糟糟的剑龙。

Plot(dist_sum(30, probs_X1))

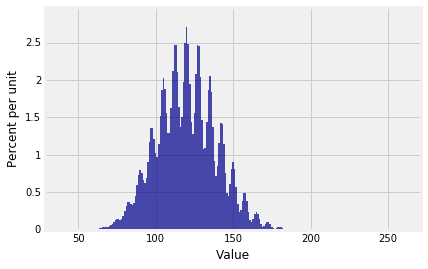
$S_{100}$的分布是：

Plot(dist_sum(100, probs_X1))

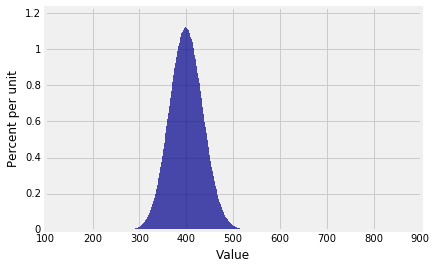
… 非常正态分布了.

这看起来好像这里有什么定理。在本章的其余部分，我们将研究该定理，该定理是关于大量独立同分布样本之和的近似分布。

请记住，只要NumPy能够处理计算,我们的pgf方法就能求出有限多个非负整数上的独立同分布样本分布总和的精确分布。在上面的例子中， $S_{100}$的pgf是一个最高次项为900的多项式。NumPy处理得很好。

中心极限定理

顾名思义，这个定理是概率，统计和数据科学领域的核心。它解释了上一节中出现的正态曲线。

在我们得到定理之前，让我们回顾一下数据8和本课程前面的一些事实。

标准单位

正如我们之前看到的，随机变量 $X$转换为标准单位如下

$$Z = \frac{X - \mu_X}{\sigma_X}$$

$Z$以标准差为单位，衡量了$X$离开均值的距离（如，均值4，标准差1,5就离开均值1个标准差的距离）。换句话说$Z$表示了$X$高于均值的标准差的数。

按线性函数规则，无论$X$的分布是什么，都有

$$E(Z) = 0 ~~~ \text{and} ~~~ SD(Z) = 1$$

标准正态曲线

回顾数据8，标准正常曲线由通常用小写希腊字母phi，$\phi$表示的函数定义，。

$$\phi(z) = \frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}z^2}, ~~~ -\infty < z < \infty$$

# HIDDEN
Plot_norm(x_limits=(-4, 4), mu=0, sigma=1)
plt.xlabel('$z$')
plt.ylabel('$\phi(z)$', rotation=0)
plt.title('Standard Normal Curve');

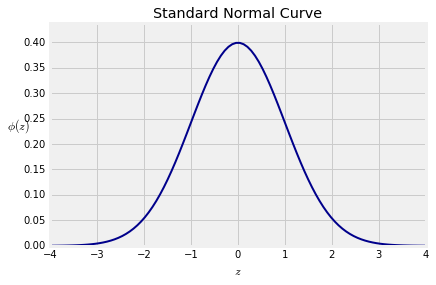
该曲线关于0对称。其拐点在$z=-1$和$z=1$。您在Data 8中观察到了这一点并且可以通过微积分证明它。

术语 我们将说曲线具有位置参数 0 和比例 参数 1。我们还将使用术语平均值来表示位置和标准差来表示比例，类似于标准单位中随机变量的均值和标准差。在本课程的后面，我们将证明这与具有连续值的随机变量的均值和标准差的定义一致。

曲线下的总面积为1。这需要一些工作来证明。您可能已经在微积分课中看到过它。我们将在课程的后期使用概率方法证明它。

如果是随机变量$X$的分布大致是钟形，那么标准化变量$Z$的分布大致遵循上面的标准正态曲线。

请注意，几乎没有概率落在范围$(-3, 3)之外。回顾一下数据8中的一下数据：

• 介于-1和1之间的面积：约68％
• 介于-2和2之间的面积：约95％
• 介于-3和3之间的面积：约99.73％

正态曲线

标准正态曲线是这样一类正态曲线，由其位置和比例参数参数，及均值和标准差确定。

均值为$\mu$，方差为$\sigma$的正态曲线定义如下：

$$f(x) ~ = ~ \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{1}{2}(\frac{x-\mu}{\sigma})^2}, ~~~ -\infty < x < \infty$$

# HIDDEN
Plot_norm(x_limits=(-4, 4), mu=0, sigma=1)
plt.xlabel('$x$')
plt.ylabel('$f(x)$', rotation=0)
plt.yticks(np.arange(0, 0.401, 0.05), np.array(7*['']))
plt.xticks(np.arange(-4, 4.1), ['','','$\mu-2\sigma$', '$\mu - \sigma$', '$\mu$', '$\mu+\sigma$','$\mu+2\sigma$',''])
plt.title('Normal Curve, mean $\mu$, SD $\sigma$');

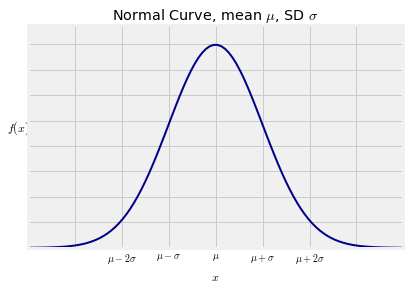
形状看起来与标准正常曲线完全相同。唯一的区别在于轴上的测量尺度。中心现在是$\mu$而不是0，并且拐点远离中心距离是以$\sigma$为单位而不是1。

现在给出正态曲线的重要性：

中心极限定理

设 $X_1, X_2, \ldots$ 是i.i.d., 每一个都有均值$\mu$和标准差$\sigma$。令$S_n = X_1 + X_2 + \cdots + X_n$，则有

$$E(S_n) = n\mu ~~~~~~~~~~ SD(S_n) = \sqrt{n}\sigma$$

我们还不知道$S_n$的分布的形状。中心极限定理（CLT）告诉我们，当$n$很大时，曲线会很平滑。

定理

当$n$很大时，标准分布的和为

$$\frac{S_n - n\mu}{\sqrt{n}\sigma}$$

无论$X_i$的分布如何，最终将大致遵循标准正态分布。

换言之，当$n$很大时，无论$X_i$的分布如何，$S_n$的分布与均值$n\mu$和标准差$\sqrt{n}\sigma$有关

中心极限定理是使用标准差对分布进行衡量的主要原因。

究竟当$n$多大时，估计值能够有一个较好的结果？这取决于$X_i$的分布。我们稍后会详细说明。现在，假设我们使用的样本大小足够大，以使正态估计合理。

该定理的证明超出了本课程的范围。但是你已经在数据8中进行的模拟以及前一节中计算的总和的精确分布中看到了大量的证据。

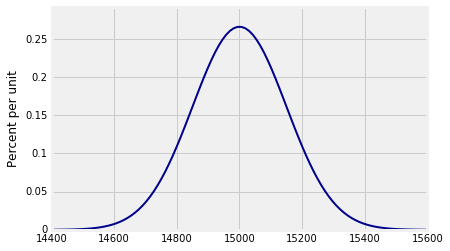
示例

假设一个样本为100人的重量，是独立同分布的，其均值为150磅，标准差为15磅。然后所采样的人的总重量的均值为$100 \times 150 = 15,000$，标准差为$\sqrt{100} \times 15 = 150$。

谁在乎一群随机人的总重量？询问那些建造体育馆，电梯和飞机的人。

您可以使用prob140方法绘制此分布Plot_norm。参数是您希望绘制曲线的间隔，平均值和标准差。

n = 100
mu = 150
sigma = 15

mean = n*mu
sd = (n**0.5)*sigma

plot_interval = make_array(mean-4*sd, mean+4*sd)

Plot_norm(plot_interval, mean, sd)

正态曲线下的概率

假设我们想要找到抽样人员的总重量小于15,100磅的概率。这大约是下面的黄金区域。这是使用正态曲线的一个估计。

请注意参数right_end=15100。这告诉Plot_norm其右边界。如果没有指定左端，则最左端视为其左边界。

Plot_norm(plot_interval, mean, sd, right_end=15100)

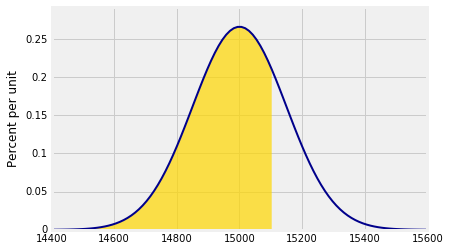
和以前一样，返回点左边所有概率的函数称为分布的累积分布函数（cdf）。stats.norm.cdf使用适当的参数，概率不到75％。

stats.norm.cdf(15100, mean, sd)

0.74750746245307709

为了估计总重量在14,800磅到15,100磅之间的概率率是多少？现在我们指定两个参数left_end和right_end：

Plot_norm(plot_interval, mean, sd, left_end=14800, right_end=15100)

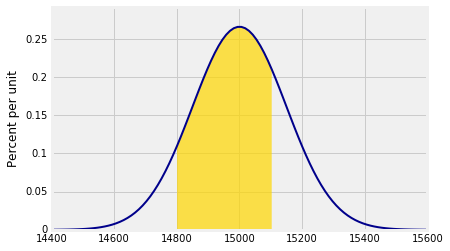
阴影面积约为65.6％.

stats.norm.cdf(15100, mean, sd) - stats.norm.cdf(14800, mean, sd)

0.65629624272720921

标准正态 CDF $\Phi$

实际上只有一条正常曲线很重要 - 标准正态曲线。所有其他的都是标准正态曲线通过水平轴的线性变换获得的。因此，通过标准化，可以根据标准正态cdf完成上述所有计算，如下所述。

要找到总重量小于15,100磅的大概几率，首先将重量标准化，然后使用标准正态cdf。

z_right = (15100 - mean)/sd

stats.norm.cdf(z_right)  # The standard curve is the default

0.74750746245307709

要找到总重量在14,800磅到15,100磅之间的概率：

z_left = (14800 - mean)/sd

stats.norm.cdf(z_right) - stats.norm.cdf(z_left)

0.65629624272720921

标准正态cdf的常用符号是大写字母$\Phi$，因为它是$\phi$的积分：

$$\Phi(x) = \int_{-\infty}^x \phi(z)dz, ~~~~ -\infty < x < \infty$$

这个积分虽然是有限的，但没有封闭形式的公式，可以用算术运算，幂，三角函数，指数和对数函数以及组合来改写。它必须通过数值积分来求近似值。这就是为什么每个统计系统都有内置功能，例如stats.norm.cdf提供出色的近似值功能。

标准化标准正态累积分布函数$\Phi$为所有正态曲线下的面积值提供了紧凑的表示法。我们不必对不同的参数使用不同的函数。

在CLT的假设下，对于大的值$n$我们有近似值

$$P(S_n \le x) ~ \approx ~ \Phi \big{(} \frac{x - n\mu}{\sqrt{n}\sigma} \big{)} ~~~ \text{for all } x$$

正如您在数据8中看到的那样，近似值通常在分布的尾部中表现不佳。如果使用CLT来逼近尾部区域的概率，请注意近似值可能非常粗糙。

二项分布 $(n, p)$ 的估计

一个二项随机分布$(n, p)$ 是$n$个i.i.d.分布的和。CLT表明，如果$n$足够大，无论$p$是什么，分布是大致成正态分布的。但我们在第6章中说过，如果$n$很大，$p$很小，那么二项分布大致是泊松分布。

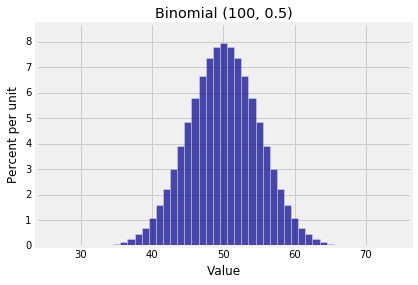
那么它到底是正态分布还是泊松分布？这是两个二项式直方图，两者都有大的$n$但有不同的形状。

k1 = np.arange(25, 76)
probs1 = stats.binom.pmf(k1, 100, 0.5)
binom_fair = Table().values(k1).probability(probs1)
Plot(binom_fair)
plt.title('Binomial (100, 0.5)');

k2 = np.arange(0, 11)
probs2 = stats.binom.pmf(k2, 100, 0.01)
binom_biased = Table().values(k2).probability(probs2)
Plot(binom_biased)
plt.title('Binomial (100, 0.1)');

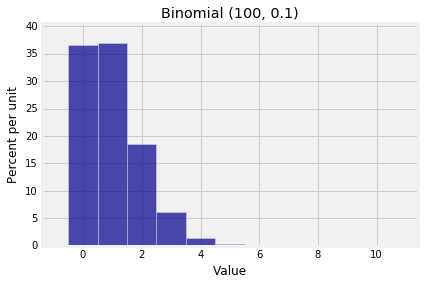
差异是由于分布的扩散。当分布在0附近时，泊松近似适用。当扩展较大时，在均值的任一侧存在大量可能值，则可以尝试正态分布。

为了量化这一点，许多文本根据给出了粗略的阈值$n$和$p$，使得，如果$n$大于阈值，那么二项式$(n, p)$大致是正态分布。如果$n$很大，二项分布类似于泊松，意味着$n$没有超过正态分布的阈值。

阈值通常以“标准差$\sqrt{npq}$大于3” 或“$np$和$nq$都大于10”来表示，这些不完全一致，但非常相近。

您可以通过比较二项式与相应泊松之间的总变化距离以及二项式与相应法线之间的总变化距离来了解您对这些阈值的看法。然而，在这个过程中，对二项式的法线与泊松近似的选择很少会成为一个问题，因为当$n$和$p$的值都给出时， 如果您对使用哪个有疑问，那么您可以使用确切的二项式概率。

这是二项式（100,0.5）分布和近似正态曲线。曲线的参数是$np = 50$和$\sqrt{npq} = 5$。

Plot(binom_fair)
Plot_norm((25, 75), 50, 5, color='red')
plt.xticks(np.arange(25, 76, 5))
plt.title('Binomial (100, 0.5) and its Normal Approximation');

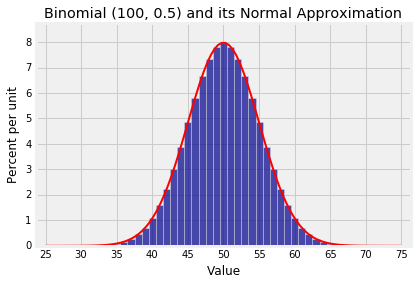
注意点“$\mbox{mean } \pm \mbox{ SD}$“$= 50 \pm 5$是曲线的拐点。

样本均值

中心极限定理的核心是什么？一个答案是它允许我们基于随机样本做出推论，即使我们对总体的分布知之甚少。

在数据8中，您看到如果我们想要估计总体的平均值，我们可以基于大随机样本的平均值来构建参数的置信区间。在该过程中，您使用引导程序生成样本均值的经验分布，然后使用经验分布来创建置信区间。你会记得那些经验分布总是钟形的。

在本节中，我们将研究样本均值的概率分布，并表明您可以使用它来构建总体均值的置信区间，而无需进行任何重新采样。

让我们从样本总和开始，我们现在很清楚。回想一下我们的假设和符号：

设$X1, X_2, \ldots, X_n$ 是一个i.i.d采样, 设每一个$X_i$的均值为$\mu$标准差为$\sigma$。设$S_n$是样本总和，即$S_n = \sum{i=1}^n X_i$。可以得到

$$E(S_n) = n\mu ~~~~~~~~~~ SD(S_n) = \sqrt{n}\sigma$$

这些结果意味着随着样本量的增加，样本总和的分布向右移动并变得更加分散。

您可以在下图中看到这一点。该图显示了5个筛子的总和和20个筛子的总和的分布。分布是精确的，使用本章前面定义的dist_sum方法计算。

die = np.append(0, (1/6)*np.ones(6))
dist_sum_5 = dist_sum(5, die)
dist_sum_20 = dist_sum(20, die)
Plots('Sum of 5 dice', dist_sum_5, 'Sum of 20 dice', dist_sum_20)

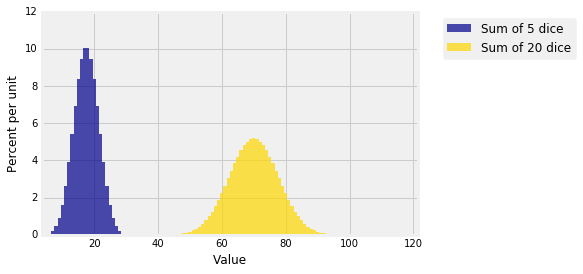
您可以看到正态分布已经显示为5和20个样本的总和。

您还可以看到黄金区域不是蓝色区域的四倍，尽管黄金区域中的样本大小是蓝色的四倍。黄金区域高只有蓝色一半，分布是蓝色的两倍。那是因为总和的标准与$\sqrt{n}$成正比。它增长比$n$慢。由于样本量大4倍，因此黄金分布的标准差为蓝色的 $\sqrt{4} = 2$倍。

样本的平均值表现不同

IID 样本的均值

设$\bar{X}_n$是样本年均值，即

$$\bar{X}_n = \frac{S_n}{n}$$

然后$\bar{X}_n$只是$S_n$的线性变换，所以

$$E(\bar{X}_n) = \frac{E(S_n)}{n} = \frac{n\mu}{n} = \mu ~~~~ \text{for all }n$$

样本均值的期望总是总体的均值$\mu$，无论样本大小。因此，无论样本大小如何，样本均值都是总体均值的无偏估计。

样本均值标准差是

$$SD(\bar{X}_n) = \frac{SD(S_n)}{n} = \frac{\sqrt{n}\sigma}{n} = \frac{\sigma}{\sqrt{n}}$$

随着样本量的增加，样本均值的变化性降低。因此，随着样本量的增加，样本均值对总体均值的估计更准确。

下图显示了5个筛子和20个筛子的平均值的分布。两者都以3.5为中心，但较大样本的均值分布较窄。您在数据8中经常看到这一点：随着样本量的增加，样本均值的分布更集中在总体均值周围。

# HIDDEN
dist_mean_5 = Table().with_columns(
    'Value', dist_sum_5.column(0)/5,
    'Probability', 5*dist_sum_5.column(1)
    )
dist_mean_20 = Table().with_columns(
    'Value', dist_sum_20.column(0)/20,
    'Probability', 20*dist_sum_20.column(1)
    )
Plots('Mean of 5 dice', dist_mean_5, 'Mean of 20 dice', dist_mean_20, width=0.2)

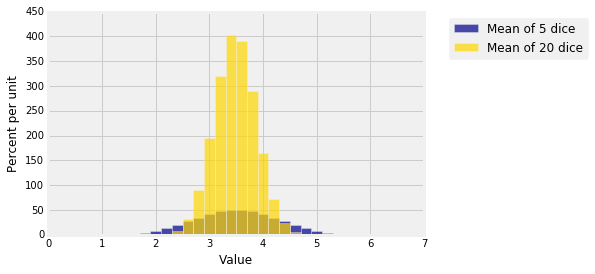
精确是有代价的。样本平均值的标准差随着样本大小的平方根减小。因此，如果要将样本均值的标准差降低3倍，则必须将样本量增加$3^2 = 9$倍。

一般结果通常可作为反例进行证明。

平方根法则

如果将样本扩大n倍，则样本均值的均值会减少$\sqrt{n}$倍。

弱大数定律

样本均值是总体均值的无偏估计，并且当样本较大时，其标准差比较小。因此，大样本的平均值接近总体平均值的概率很高。

这一结论称为弱大数定律。

令$X_1, X_2, \ldots, X_n$是i.i.d.，每一个有均值$\mu$和标准差$\sigma$，令$\bar{X}_n$是样本均值。取一个极小数$\epsilon > 0$，有

$$P(|\bar{X}_n - \mu| < \epsilon) \to 1 ~~~ \text{as } n \to \infty$$

也就是说，对于$n$取值很大时，几乎可以确定均值在$\mu \pm \epsilon$的范围内，

为了证明该定律，我命将证明$P(|\bar{X}_n - \mu| \ge \epsilon) \to 0$，这是用切比雪夫不等式很容易求解。

$$P(|\bar{X}_n - \mu| \ge \epsilon)~ \le ~ \frac{\sigma_{\bar{X}_n}^2}{\epsilon^2} ~ = ~ \frac{\sigma^2}{n\epsilon^2} ~ \to ~ 0 ~~~ \text{as } n \to \infty$$

相关定律

• 强大数定律。 这表示在概率为1时，样本平均值收敛到极限，并且该极限是常数$\mu$。请参阅Fields Medalist Terence Tao撰写的这篇博客文章。他陈述了基础标准差可能不存在的情况下的定律情况。请注意，我们的弱大数定律证明方法在这种情况下无效; 结果仍然是正确的，但证据需要更多的探索。
• 小数定律。 这是Ladislaus Bortkiewicz (1868-1931)一本书的标题。其中他描述了低概率事件分布的泊松近似。这就是为什么这些注释的第6.4节被称为小数定律。
• 平均定律。 在总体是二元的情况下，这是弱法则的通用名称，样本均值只是样本中成功的比例。在通常的使用中，人们有时会忘记定律是一种限制性陈述。如果你正在抛硬币并连续看到10个正面，那么下一个抛正面的机会仍然是1/2。平均律并没有说你“应该是反面”。它不适用于有限的投掷集。

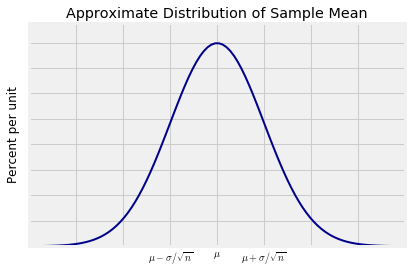
分布的形状

中心极限定理告诉我们，对于大样本，样本均值的分布大致是正态的。样本均值是样本和的线性变换。因此，如果样本总和的分布大致是正态的，则样本均值的分布也大致是正态的，但具有不同的参数。具体来说，对于$n$很大的情况下

$$P(\bar{X}_n \le x) ~ \approx ~ \Phi \big{(} \frac{x - \mu}{\sigma/\sqrt{n}} \big{)} ~~~~ \text{for all } x$$

# HIDDEN
Plot_norm(x_limits=(-4, 4), mu=0, sigma=1)
plt.yticks(np.arange(0, 0.401, 0.05), np.array(7*['']))
plt.xticks(np.arange(-4, 4.1),['','','','$\mu - \sigma/\sqrt{n}$', '$\mu$', '$\mu+\sigma/\sqrt{n}$','',''])
plt.title('Approximate Distribution of Sample Mean');

置信区间

假设你有一个大的iid样本。CLT意味着有约95％的概率，样本均值在总体平均值的2个标准差距离内。

# HIDDEN
Plot_norm(x_limits=(-4, 4), mu=0, sigma=1, left_end=-2, right_end=2)
plt.yticks(np.arange(0, 0.401, 0.05), np.array(7*['']))
plt.xticks(np.arange(-4, 4.1),['','','$\mu - 2\sigma/\sqrt{n}$', '', '$\mu$', '', '$\mu+2\sigma/\sqrt{n}$',''])
plt.xlabel('Sample Mean')
plt.title('Gold Area: Approximately 95%');

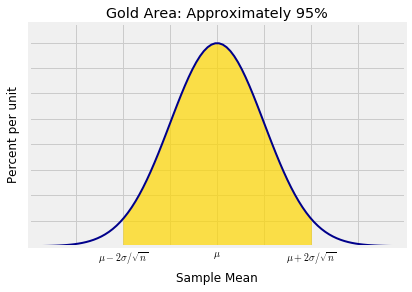
这可以用不同的方式表达：

• 在所有样本集合的约95％的样本中，样本平均值在总体平均值$\pm ~ 2 \sigma/\sqrt{n}$的范围内。

换言之：

• 在所有样本集合的约95％的样本中， 总体的平均值在样本均值 $\pm ~ 2 \sigma/\sqrt{n}$的范围内。

这就是为什么用样本均值$\pm ~ 2 \sigma/\sqrt{n}$作为$\mu$的估计间隔。

$\mu$的置信区间

样本均值$\pm ~ 2 \sigma/\sqrt{n}$的区间称之为参数$\mu$的95％置信区间这个区间，拥有一个95%的置信水平。

你可以选择不同的置信水平，比如说80％。在这个选择下，你的期望区间会更窄。要确切了解中心两侧需要多少标准差的距离，来获得大约80％的中心区域，您必须找到在标准正态曲线上相应的$z$，如下图所示。

# HIDDEN
Plot_norm(x_limits=(-4, 4), mu=0, sigma=1, left_end=-1.28, right_end=1.28)
plt.yticks(np.arange(0, 0.401, 0.05), np.array(7*['']))
plt.xticks(make_array(-1.28, 0, 1.28),['$-z$', '0', '$z$'])
plt.title('Gold Area: Approximately 80%');

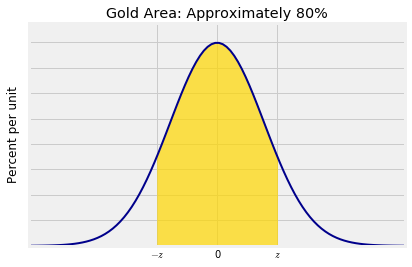
正如您从数据8中所知，并且可以在图中看到，间隔从分布的第10百分位到第90百分位。所以$z$是标准正态曲线的第90个百分点，也称为曲线的“90％点”。scipy方法会调用ppf并将f分位数的十进制值作为其参数。

stats.norm.ppf(.9)

1.2815515655446004

因此，总体的大约80％置信区间意味着总体均值$\mu$在”样本均值 $\pm ~ 1.28\sigma/\sqrt{n}$”范围内。

让我们仔细校验，2是$z$的一个很好的取值，这意味着95％的置信区间。该$z$我们需要的是97.5％的点数：

stats.norm.ppf(.975)

1.959963984540054

那是$z = 1.96$，这就是我们一直使用的2。这个值已经足够了，但是$z = 1.96$也常用于构建95％置信区间。

一般定义

设$\lambda$是一个置信水平，令$z\lambda$代表了这样一个分位数，使得正态曲线中，$(-z\lambda, ~ z\lambda)$包含了$\lambda$%区域。在上面的例子中，$\lambda$的值是80， $z\lambda$的值是1.28。

当$n$足够大时，有

$$\frac{\lambda}{100} ~ \approx ~ P(\bar{X}_n \in \mu ~ \pm ~ z_\lambda \sigma/\sqrt{n}) ~ = ~ P(\mu \in \bar{X}_n ~ \pm ~ z_\lambda \sigma/\sqrt{n})$$

随机区间$\bar{X}n ~ \pm ~ z\lambda \sigma/\sqrt{n}$被称为总体均值$\mu$的$\lambda$%置信区间。这意味着，大约有$\lambda$%的概率，该随机区间包含$\mu$。

不同级别的置信区间之间的唯一区别是$z$的选择，这取决于置信水平。另外两个组成是样本均值和标准差。

复习数据8中的示例

让我们回到数据8中非常熟悉的一个例子：1,174对母亲及其新生儿的随机样本。

baby = Table.read_table('baby.csv')

baby

Birth Weight	Gestational Days	Maternal Age	Maternal Height	Maternal Pregnancy Weight	Maternal Smoker
120	284	27	62	100	False
113	282	33	64	135	False
128	279	28	64	115	True
108	282	23	67	125	True
136	286	25	62	93	False
138	244	33	62	178	False
132	245	23	65	140	False
120	289	25	62	125	False
143	299	30	66	136	True
140	351	27	68	120	False

... (1164 rows omitted)

第三栏包括母亲的年龄。让我们为总体中母亲的平均年龄构建大约95％的置信区间。我们在Data 8中使用bootstrap完成了这项工作，因此我们有了能够进行比较的结果。

因为我们的数据来自大型随机样本，我们可以应用本节的方法。

n = 1174
ages = baby.column('Maternal Age')

samp_mean = np.mean(ages)
samp_mean

27.228279386712096

可以发现样本的$\bar{X}_n$值是27.23。我们知道$n = 1174$，所以，我们需要总体的标准差$\sigma$然后就可以完成我们的计算。

但是，我们当然不知道总体的标准差$\sigma$。

所以，我们使用数据来估计$\sigma$，当然，这个估计存在一些误差，但它除以 $\sqrt{n}$后，误差会被缩小。请记住，我们的方法依赖于CLT，仅在$n$很大时有效。

$\sigma$的估计大约是5。82年。

sigma_estimate = np.std(ages)
sigma_estimate

5.8153604041908968

一个总体的95%置信区间是$(26.89, 27.57)$。

samp_mean - 2*sigma_estimate/(n**0.5), samp_mean + 2*sigma_estimate/(n**0.5)

(26.888831911866099, 27.567726861558093)

不需要bootstrapping了!

现在让我们比较两种方法的结果。调用Data 8的bootstrap_mean方法。

def bootstrap_mean(original_sample, label, replications):
    
    """Displays approximate 95% confidence interval for population mean.
    original_sample: table containing the original sample
    label: label of column containing the variable
    replications: number of bootstrap samples
    """
    just_one_column = original_sample.column(label)
    n = len(just_one_column)
    means = make_array()
    for i in np.arange(replications):
        bootstrap_sample = np.random.choice(just_one_column, size=n)
        resampled_mean = np.mean(bootstrap_sample)
        means = np.append(means, resampled_mean)
        
    left = percentile(2.5, means)
    right = percentile(97.5, means)
    
    resampled_means = Table().with_column(
    'Bootstrap Sample Mean', means
    )
    resampled_means.hist(bins=15)
    print('Approximate 95% confidence interval for population mean:')
    print(np.round(left, 2), 'to', np.round(right, 2))
    plt.plot(make_array(left, right), make_array(0, 0), color='yellow', lw=8);

让我们为总体平均值构建95％置信区间的bootstrap。我们将使用5000引导样本，就像我们在Data 8中所做的那样。

bootstrap_mean(baby, 'Maternal Age', 5000)

Approximate 95% confidence interval for population mean:
26.9 to 27.57

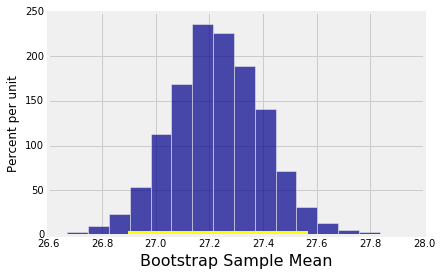
bootstrap置信区间与我们使用正态近似得到的区间（26.89,27.57）基本相同。

正如我们在数据8中所做的那样，我们观察到样本中母亲年龄的分布远非正态分布：

baby.select('Maternal Age').hist()

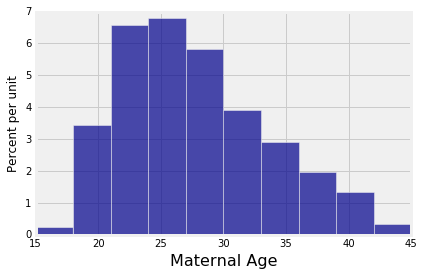
但是，样本均值的经验分布，显示为前一个单元格的输出，大致为钟形。这是因为由中心极限定理可得，大样本的平均值的概率分布是近似正态的。